Grafické interpretace výsledků maturitní zkoušky

Jednou z možností interpretace výsledků zkoušky je zobrazení v grafech. S jejich pomocí je mnohem snazší vyčíst souvislosti, které by se z izolovaných stavových veličin v tabulce velmi obtížně dedukovaly.

Zkouška z českého jazyka a literatury byla pro všechny žáky povinná. Ve druhé dílčí zkoušce si žáci vybírali jednu z možností: cizí jazyk nebo matematiku. V prvním grafu jsou uvedeny výsledky žáků jedné třídy, kde se 40 % žáků přihlásilo ke zkoušce z cizího jazyka a zbývajících 60 % žáků ke zkoušce z matematiky. Jeden přihlášený žák zkoušku z matematiky nekonal.

V prvním grafu jsou zobrazeny výsledky všech žáků. Jsou uspořádány vždy od nejslabšího po nejlepší výkon měřený % úspěšnosti. Červené sloupce představují výsledky žáků v cizím jazyce (čím vyšší je sloupec, tím lepší je výsledek), modré sloupce výsledky žáků v matematice.

V následujících úvahách se budeme věnovat jen jedné zkoušce, proto červené sloupce nahradíme prázdným obdélníkem. V grafu je tak zachována informace, že 40 % žáků bylo přihlášeno ke zkoušce z cizího jazyka a zbývajících 60 % žáků ke zkoušce z matematiky.

Další zjednodušení představuje třetí graf. Není nutné pro každého žáka vykreslovat samostatný sloupec, ale postačí obrys, který zachovává veškeré potřebné informace: výsledky žáků v matematice (hodnoty úspěšnosti v % lze vyčíst na svislé ose), informaci o počtu žáků (resp. podílu žáků v %), kteří si vybrali zkoušku z matematiky, i informaci o podílu přihlášených žáků, kteří ke zkoušce nenastoupili (krátký rovný úsek na vodorovné ose).

Prostřednictvím takto sestrojených grafů lze posuzovat výsledky žáků v různých skupinách (tzv. entitách), např. výsledky žáků v jednotlivých školách, v krajích, v celé ČR, a to i po jednotlivých oborech.

Popis grafu:

V grafu jsou výsledky maturitní zkoušky z matematiky v celé ČR. Vidíme, že přihlášeno bylo kolem 40 % žáků (cizí jazyk přibližně 60 %), ale nezanedbatelná část (asi 5 % maturantů) ke zkoušce z matematiky ani nenastoupila. Červená čára představuje 33% minimální požadovanou hranici pro úspěšné vykonání zkoušky, tzv. Cut off score (COS). Šířka zeleného pole pod minimální hranicí úspěšnosti představuje procento maturantů, které u maturity neuspělo kvůli matematice (asi 7,5 %).

V poslední době roste poptávka po srovnávání škol, tříd, krajů nebo jednotlivých oborů a velké oblibě se těší tzv. žebříčky. Dosud publikované žebříčky jsou velmi diskutabilní, neboť ve většině případů používají jedinou stavovou hodnotu, např. průměrnou úspěšnost, a vůbec nezohledňují další veličiny, které ovlivňují samotné podmínky maturitní zkoušky. V současné době je ve společné části maturitní zkoušky skupina volitelných předmětů a díky rozdílným preferencím žáků dochází k nerovnoměrnému rozdělení žáků mezi tyto nabízené předměty. Samotná průměrná úspěšnost tuto skutečnost nepostihne a ani opačná snaha o tvorbu nejrůznějších funkcí vytvořených z několika parametrů zpravidla nevede k věrohodnému obrazu skutečnosti. Pokud se však dokážeme zorientovat v předkládaných datech, můžeme získat velmi dobrý obraz o skutečnosti.

Vše lze demonstrovat na zpracování výsledků několika entit prostřednictvím tabulky a grafu.

Průměrná úspěšnost je nejběžnější údaj, který se používá při tvorbě žebříčků. Všimněme si, že je vypočtena z různě rozsáhlých skupin žáků. Srovnávat lze však jen skupiny s přibližně stejným podílem volby předmětu. Např. porovnání prvních dvou gymnázií na základě průměrné úspěšnosti je chybné. (Pokud byste chtěli u dvou tříd porovnávat např. výšku žáků, nemůžete v jedné třídě počítat průměr ze 40 % nejvyšších žáků a ve druhé skupině téměř ze 70 % žáků.) Rovněž lze usoudit, že přibližně čtvrtina žáků přihlášených ke zkoušce z matematiky je z gymnázií. Z tabulky lze s jistotou tvrdit, že žáci z gymnázií jsou k maturitě z matematiky lépe připraveni než průměrný maturant z ostatních typů škol. Obě gymnázia pak rozhodně patří k těm výrazně úspěšnějším.

Před porovnáním průměrných úspěšností si tedy zkontrolujte, zdali je podíl volby předmětu u obou skupin přibližně stejný. Směrodatná odchylka vyjadřuje průměrné rozdíly mezi žáky konajícími maturitní zkoušku. Čím vyšší je toto číslo, tím větší jsou disproporce mezi žáky. Medián je zajímavé posuzovat ve vztahu k průměru. Je-li medián větší než průměr, mezi podprůměrnými žáky budou větší rozdíly než mezi nadprůměrnými žáky (sklon křivky zobrazující úspěšnosti bude u slabších žáků strmější). Je-li medián menší než průměr, situace bude opačná. Z počtu přihlášených a podílu volby lze usuzovat, jedná-li se např. jen o jednu třídu (Gymnázium A), nebo o více tříd (3 třídy gymnázia B).

Z grafů lze vyčíst mnohem více informací než z tabulky.

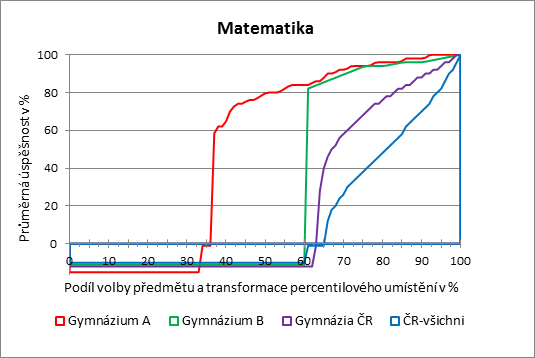
Před další argumentací provedeme pro zasvěcené ještě jednu odbornější instruktáž ke grafu. Nejprve vysvětlení zobrazovací soustavy. Veličinou, která je zobrazována vodorovnou osou, je tzv. transformované percentilové umístění. Je provedeno tak, že všem žákům, kteří nekonali zkoušku z matematiky, ale konali zkoušku z cizího jazyka, resp. ke zkoušce nenastoupili, jsou přiděleny záporné, resp. nulové hodnoty procentních bodů. Na takto "obohacené" skupině dat lze pracovat s percentily běžným způsobem. Každá z křivek průměrné úspěšnosti je vystavěna nad základnou 0 – 100 % a představuje všechny žáky, kteří se v rámci dané entity hlásili k druhé povinné zkoušce společné části maturitní zkoušky. Vlastní porovnávání průměrných úspěšností se však týká jen jednoho předmětu, v tomto případě matematiky. Pro názorné zachycení této skutečnosti jsou proto v grafu zobrazeny pod vodorovnou osou úsečky odpovídající procentu žáků, kteří si v rámci dané entity matematiku jako druhou povinnou zkoušku nezvolili. Podíváme-li se tedy na modrou křivku, která přestavuje průměrnou školu v rámci celé České republiky, vidíme, že hodnoty nula a vyšší, tedy hodnoty úspěšnosti v matematice, začínají na pozici cca 60. To znamená, že cca 60 % žáků si v rámci ČR zvolilo jako druhý předmět cizí jazyk a cca 40 % matematiku. Pokud nahlédneme do tabulky statistických parametrů datových vzorků do sloupce "% přihlášených", zjistíme, že přesný podíl přihlášených matematik je 39 %. Tato zobrazovací metoda je použita pro všechny ostatní entity. Můžeme tak například zjistit, že se přihlásilo k matematice 37 % gymnazistů, v Gymnáziu A pak 67 % a v Gymnáziu B 39 %. Počty přihlášených jsou údaje zřejmé stejně jako ostatní statistické hodnoty.

Tedy velmi silnou účast v matematice mělo Gymnázium A (téměř dvojnásobná účast oproti průměrnému gymnáziu). Z grafu je patrné, že žáci zbývajících tří entit tíhnou spíše k cizím jazykům. Kolem 5 % žáků ČR přihlášených k maturitě z matematiky ke zkoušce vůbec nenastoupilo (rovný úsek na vodorovné ose). Rovněž několik přihlášených žáků z Gymnázia A ke zkoušce z matematiky nenastoupilo. Podíl těchto žáků na gymnáziích ČR je spíše zanedbatelný. Nejkompaktnější skupina, která konala maturitu z matematiky, byla na Gymnáziu B, naopak mezi žáky ČR jsou velmi výrazné rozdíly.

Vyslovme nyní hypotézu o pořadí úspěšnosti srovnávaných škol (Gymnázium A a Gymnázium B). Žáci Gymnázia A dosáhli v matematice průměrné úspěšnosti (jak ukazuje údaj v tabulce) 87,4 %. Žáci Gymnázia B dosáhli průměrné úspěšnosti 92,9 %. Zdá se tedy, že podle průměrné úspěšnosti je Gymnázium B lepší. Je tomu ale skutečně tak? Na první pohled, porovnáme-li křivky dosažených průměrných úspěšností, tomu tak není. Veličinou průměrné úspěšnosti totiž porovnáváme neporovnatelné. Průměrná úspěšnost žáků Gymnázia B je totiž počítána z výsledků 39 % přihlášených žáků, zatímco u Gymnázia A je tatáž veličina počítána pro 68 % přihlášených žáků. Zdá se, minimálně z tohoto pohledu, spravedlivé a poctivé porovnávat pouze průměrnou úspěšnost, když už, pouze na srovnatelné procentní skupině přihlášených žáků. Pokud tak učiníme, je z grafu na první pohled vidět, že v celém úseku vymezeném křivkou Gymnázia B jsou hodnoty dosažených průměrných úspěšností žáků Gymnázia A srovnatelné, resp. o něco vyšší. Které z gymnázií je tedy lepší?

Nad uvedeným grafem můžeme s jistotou říci, že obě gymnázia jsou výrazně nad průměrem krajským i republikovým. Určitě dále platí, že na Gymnáziu A je matematika předmětem preferovaným před cizími jazyky, a je jí možná věnováno více prostoru, možná má větší počet kvalitních motivujících učitelů, atd. Určitě by tento pohled měl vyvolat minimálně vážnou pochybnost o smysluplnosti jakýchkoli snah o zjednodušené "žebříčkování".